I think it did it pretty good job for what I set out to accomplish. I wanted to know how a pitcher pitched over a given season, and along with the pitchers K%, BB%, and batted ball quality, we could see exactly why a pitcher was either succeeding or having troubles. For that reason, it also served as a good benchmark for the question of “who got lucky and who got unlucky”.

The issue was, of course, it didn’t tell us a “true skill” level of the pitcher. Given what we know about the unreliability of xStats, it’s very possible that a not so great pitcher allowed a lot of poor contact over the course of a season (and vice versa), had a really good xwOBA (and thus CRA), and then regressed back to a not-so-great pitcher the following year. So my next steps were to move towards creating something that was a bit more predictable.

Enter Barrels

One thing we know for sure is how much quicker barrels become reliable when compared to xwOBA and similar, all-inclusive “expected” stats. For pitchers, barrels don’t stabilize nearly as quickly as they do for hitters, but they are much more of a “skill” measurement for than xwOBA is. In a 2016 study, Russell A. Carleton found that “reliability peaked for barrel rate for pitchers around 400 balls in play with a Kuder-Richardson coefficient of .58”, where 0.7 is the typical benchmark for “stable”.

Luckily, barrels per batted ball event (Brls/BBE) and xwOBA on contact go hand in hand pretty well, so we don’t have to completely change the design of CRA or do any assuming we don’t want to (which was the primary goal of CRA in the first place).

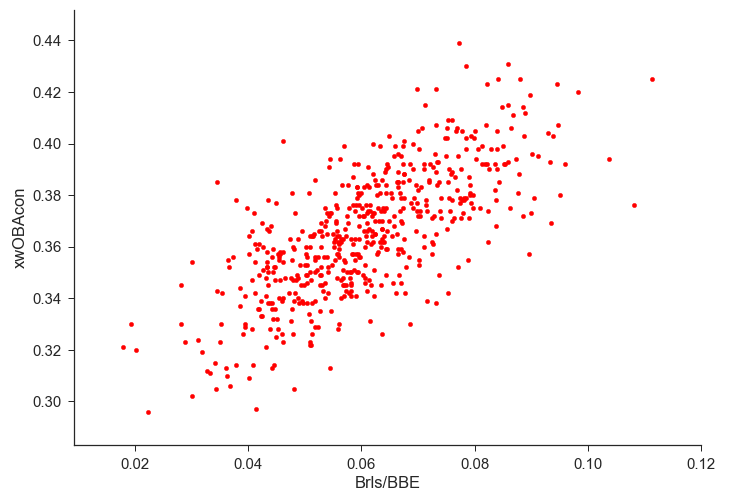
“Predictive” CRA (pCRA)

With the inclusion of Barrels and subtraction of xwOBA, we’ll hopefully get a much better estimator for true pitcher skill. Along with barrels, this new predictive iteration of CRA (pCRA) also takes another batted ball classification in combination with a design feature taken from SIERA, which is that pitchers who walk more hitters but also keep balls on the ground will induce more double plays. By separating barrels from the rest of xwOBA, we will hopefully remove some of the more heavily varying aspects of it.

The results? Some of the best ERA prediction in the Statcast Era.

As I did with the descriptive CRA (let’s call this dCRA from now on, for the sake of ease), we take a look at each of the root mean squared errors (RMSE) for each of the best and most often used ERA estimators available, such as FIP, xFIP, and SIERA. Those RMSEs will tell us the average error in each of the model’s predicted values for next season’s ERA. For a minimum of 40 IP in back to back years, the RMSE to the next season’s ERA were as follows:

ERA – 1.445  | FIP – 1.256  | xFIP – 1.154 |  SIERA – 1.140 | pCRA – 1.133

It’s a small difference, but a difference in favor of pCRA nonetheless, and the miniscule difference you see here (with a 40 IP threshold) is actually one of the smaller ones when you compare it to different samples of IP totals in consecutive years. Here are each of those RMSEs as the IP totals in back-to-back years increase.

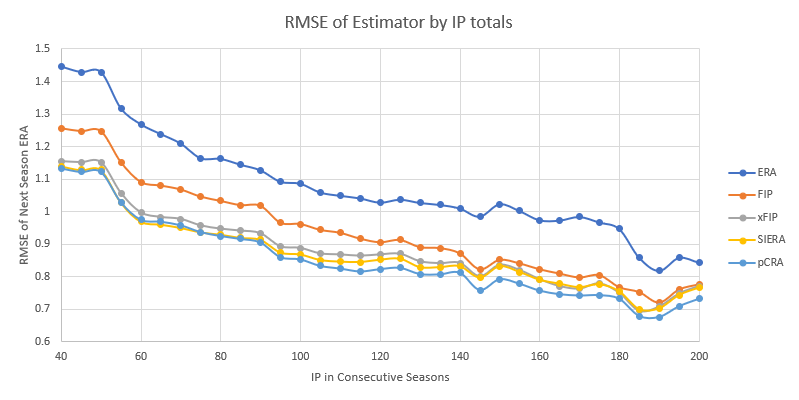
In the years we have data for (2015-2018), pCRA is better than xFIP, plain and simple. At no point across any of the consecutive year IP thresholds does xFIP do a better job predicting ERA than pCRA does.

The error in pCRA and SIERA stay very close to one another from about 40-80 IP in consecutive years, but around the 80 IP mark, the average error from pCRA to next season’s ERA dips below that of the SIERA error and never looks back. On average, from 120+ IP in back-to-back years, pCRA predicts next season’s ERA 3-4% better than SIERA, a noticeable amount. This makes sense given that 120 IP is roughly the point in which a pitcher would being to approach that “peak reliability” of 400 BBE that Carleton found in his study.

Stickiness

One thing I failed to examine in my initial CRA column is the “stickiness” of it – how much does a pitcher’s CRA change from one year to the next? No metric should stay perfectly static, as players are continuously changing, but as we strive towards finding a “true skill” level for a given pitcher, intuitively, it makes sense that we wouldn’t want said metric to fluctuate much from year to year. Otherwise, why is it better than ERA, which is fluctuates heavily year to year in a lot of cases?

One thing I know for sure is that dCRA (the old one) would not have been very sticky, because of the unreliable nature of xwOBA. pCRA, however, is a different story. Again, for all pitchers who pitched 40 IP in back-to-back years from 2015 to 2018, the average difference in each metric YoY was as follows:

ERA – 1.445  | FIP – 1.029  | xFIP – 0.733 |  SIERA – 0.707 | pCRA – 0.684

Again, it’s a very small difference in favor of pCRA, but another point for those keeping score at home. Even if you bump those minimum IP’s up to 80 and 120, pCRA is still the stickiest year over year:

80 IP:

ERA – 1.162  | FIP – 0.82  | xFIP – 0.577  | SIERA – 0.572 |  pCRA – 0.529

120 IP:

ERA – 1.028  | FIP – 0.744  | xFIP – 0.558 |  SIERA – 0.548 | pCRA – 0.512

Down to half a run in average stickiness from year to year at 120+ IP. What we have here with pCRA is a huge success. Between the lowest error in predicting next season’s ERA and the stickiest metric we’ve measured here, pCRA could be the best pitcher estimator in the Statcast Era.

Now, considering the test sample of pCRA is confined to the Statcast Era due to the inclusion of barrels, we unfortunately can’t test any data earlier than this, hence why I haven’t dubbed it to be the best estimator ever (that would be a silly claim anyway – all estimators can be useful to shed different types of information). Should we have the ability to get barrel data before 2015, we could test pCRA against its counterparts more in depth and we could get much different results, especially what we know about the way the game has evolved in the last 10 years.

For now, however, it seems that pCRA does the best job in giving us a true “pitcher skill” mark, even if it is only better than SIERA by ever so slightly.

Leaders for 2019